3. Interpolación de Lagrange#

En este apartado, se presenta otra forma de resolver el problema de interpolación polinómica que ya vimos en el primer tema usando la matriz de Vandermonde, que resulta ser más eficiente desde el punto de vista de la obtención de esquemas numéricos para la solución de ecuaciones diferenciales.

Se consideran \(N + 1\) puntos \(\{x_0, x_1, \ldots , x_N\}\) del dominio de definición de una función \(f(x)\), en los que se conocen los valores que toma la función: \(f(x_j) = y_j , \quad j = 0, 1, \ldots , N\).

A continuación, se expresa el polinomio \(I_N\) de grado \(\leq N\), en la forma siguiente:

(3.1)#\[\begin{equation} I_N (x) = b_{0} \ \ell_{0} (x) \ + \ b_{1} \ \ell_{1} (x) \ + \ \cdots \ + \ b_{N} \ \ell_{N} (x) , \end{equation}\]

donde \(\{b_{0}, b_{1}, \ldots , b_{N}\}\) son coeficientes a calcular y \(\ell_j (x)\) son polinomios de grado \(N\), que tienen la expresión siguiente:

(3.2)#\[\begin{equation} \displaystyle \ell_{j} (x) \ = \ \frac{(x - x_0)(x - x_1) \ldots (x - x_{j - 1} )(x - x_{j + 1}) \ldots (x - x_N)} {(x_j - x_0)(x_j - x_1) \ldots (x_j - x_{j - 1} )(x_j - x_{j + 1}) \ldots (x_j - x_N)} \ = \ \displaystyle \overset{N}{\underset{\begin{subarray}{l} i = 0 \\ i \neq j \end{subarray} }{\prod}} \ \frac{(x - x_i)}{(x_j - x_i)} . \end{equation}\]

La forma \(I_N (x)\) se conoce como interpolación de Lagrange y los polinomios \(\ell_{j} (x)\) son los polinomios de Lagrange. Esta forma de interpolación puede expresarse, de forma compacta, como se indica a continuación: $\( \displaystyle I_N (x) \ = \ \sum_{j = 0}^N \ b_j \ \displaystyle \overset{N}{\underset{\begin{subarray}{l} i = 0 \\ i \neq j \end{subarray} }{\prod}} \ \frac{(x - x_i)}{(x_j - x_i)} . \)$

Una característica fundamental de los polinomios de Lagrange es que verifican:

(3.3)#\[\begin{equation} \left\{ \begin{array}{l} \ell_j (x) = 1 , \qquad x = x_j , \\ \ell_j (x) = 0 , \qquad x = x_i , \qquad i = 0, 1, \dots, j-1, j+1, \dots, N . \end{array} \right. \label{valores_polinomios_Lagrange} \end{equation}\]

Esa propiedad nos va a permitir calcular muy facilmente los coeficientes \(\{b_i\}\).

Para cada uno de los puntos de interpolación, se pueden plantear las expresiones siguientes:

(3.4)#\[\begin{equation} \left\{ \begin{array}{l} b_0 \ \ell_0 (x_0) \ + \ b_1 \ \ell_1 (x_0) \ + \ \cdots \ + \ b_N \ \ell_N (x_0) \ = \ f (x_0) , \\ b_0 \ \ell_0 (x_1) \ + \ b_1 \ \ell_1 (x_1) \ + \ \cdots \ + \ b_N \ \ell_N (x_1) \ = \ f (x_1) , \\ \hspace{1cm} \vdots \\ b_0 \ \ell_0 (x_N) \ + \ b_1 \ \ell_1 (x_N) \ + \ \cdots \ + \ b_N \ \ell_N (x_N) \ = \ f (x_N) , \end{array} \right. \end{equation}\]

que, haciendo uso de la propiedad anterior resultan:

\[ b_0 \ = \ f (x_0) , \qquad b_1 \ = \ f (x_1), \qquad \ldots \qquad , b_N \ = \ f (x_N) , \]

con lo que, el polinomio interpolante, resulta ser:

\[ I_N (x) \ = \ f (x_0) \ \ell_0 (x) \ + \ f (x_1) \ \ell_1 (x) \ + \ \cdots \ + \ f (x_N) \ \ell_N (x) , \]

y que, en forma compacta, tiene la expresión siguiente:

(3.5)#\[\begin{equation} \displaystyle I_N (x) \ = \ \sum_{j = 0}^N \ f (x_j) \ \ \displaystyle \overset{N}{\underset{\begin{subarray}{l} i = 0 \\ i \neq j \end{subarray} }{\prod}} \ \frac{(x - x_i)}{(x_j - x_i)} . \label{Interpolacion_Lagrange} \end{equation}\]

Por tanto, se observa que para resolver el problema de interpolación polinómica, mediante el método de Lagrange, no es necesario resolver un sistema lineal de ecuaciones algebraicas, ya que los coeficientes son los valores de la función a interpolar en los puntos de interpolación \(f (x_0), f (x_1), \ldots , f (x_N)\), que son datos del problema.

A continuación se presenta un ejemplo de interpolación en la forma de Lagrange, con tres puntos de interpolación.

  • Ejemplo:
    Dada una función \(f(x)\) y 3 puntos de interpolación \(\{x_0, x_1, x_2\}\) en su dominio de definición, se propone obtener el polinomio interpolante \(I_2\), de grado \(\leq 2\), mediante la interpolación de Lagrange, que verifique que:

\[ I_2 (x_0) \ = \ f (x_0) \ = \ y_0 , \qquad I_2 (x_1) \ = \ f (x_1) \ = \ y_1 , \qquad I_2 (x_2) \ = \ f (x_2) \ = \ y_2 . \]

Aplicando la fórmula para hallar el polinomio interpolador por Lagrange, el interpolante de grado \(\leq 2\) es:

\[ I_2 (x) \ = \ b_0 \ \ell_0 (x) \ + \ b_1 \ \ell_1 (x) \ + \ b_2 \ \ell_2 (x) , \]

donde \(\{\ell_0, \ \ell_1, \ \ell_2\}\) son polinomios de grado \(\leq 2\) que tienen las expresiones siguientes:

\[\begin{split} \begin{array}{l} \displaystyle \ell_0 (x) \ = \ \frac{(x - x_1)(x - x_2)}{(x_0 - x_1)(x_0 - x_2)} , \\ \displaystyle \ell_1 (x) \ = \ \frac{(x - x_0)(x - x_2)}{(x_1 - x_0)(x_1 - x_2)} , \\ \displaystyle \ell_2 (x) \ = \ \frac{(x - x_0)(x - x_1)}{(x_2 - x_0)(x_2 - x_1)} . \end{array} \end{split}\]

Se puede comprobar facilmente que los polinomios anteriores verifican:

\[\begin{split} \begin{array}{l} \ell_0 (x_0) \ = \ 1 , \quad \ell_0 (x_1) \ = \ 0 , \quad \ell_0 (x_2) \ = \ 0 , \\ \ell_1 (x_0) \ = \ 0 , \quad \ell_1 (x_1) \ = \ 1 , \quad \ell_1 (x_2) \ = \ 0 , \\ \ell_2 (x_0) \ = \ 0 , \quad \ell_2 (x_1) \ = \ 0 , \quad \ell_2 (x_2) \ = \ 1 . \end{array} \end{split}\]

Finalmente, los coeficientes del interpolante son \(b_0 \ = \ f (x_0) , \ b_1 \ = \ f (x_1) , \ b_2 \ = \ f (x_2)\), que son datos del problema. El polinomio buscado es:

\[ I_2 (x) \ = \ f (x_0) \ \ell_0 (x) \ + \ f (x_1) \ \ell_1 (x) \ + \ f (x_2) \ \ell_2 (x) . \]

Vamos a resolverlo en un código simple

# Importamos los módulos necesarios
import numpy as np 
import scipy as sp
import matplotlib.pyplot as plt

"""
Puntos de interpolación
(1,2); (2.5, 7.); (4., 3.)
"""

x_i = np.array([1., 2.5,4.])
y_i = np.array([2., 7., 3.])

# Polinomio de Lagrange L_j(x)
def L_j(j, x_i, x):
    n = np.size(x_i)
    Lj = 1.
    for i in range(n):
        if i!=j: Lj *= (x-x_i[i])/(x_i[j]-x_i[i]) 
    return Lj

def I_N(x, x_i, y_i):
    n = np.size(x_i)
    S = 0.
    for i in range(n):
        S += y_i[i]*L_j(i, x_i, x)
    return S

"""
Para visualizar la función genero una gráfica con los puntos de interpolación junto con el valor del
polinomio interpolador en un conjunto de puntos dentro del dominio de definición.
"""

x = np.linspace(min(x_i)-1, max(x_i)+1, 100)

### Representación gráfica
ax = plt.scatter(x_i,y_i, color="red")
plt.plot(x,I_N(x, x_i, y_i), color="blue")

plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title('Interpolante polinómico de Lagrange', fontsize=16)

Text(0.5, 1.0, 'Interpolante polinómico de Lagrange')
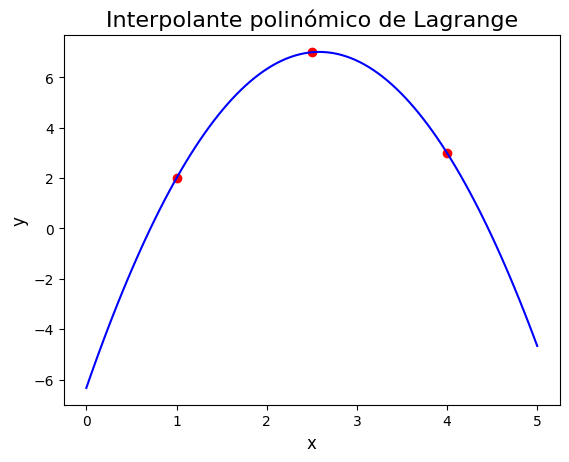
../../_images/4add5448b89ada259bb597aaaa799697f38dc36f0349f4a7d7a963f378e40e92.png

Podemos utilizar la función scipy.interpolate.lagrange(x,y) que devuelve la forma analítica del polinomio interpolador de Lagrange. En el caso de antes este será:

\[ I_N(x) = -2x^2 + 10.33x -6.333 \]
from scipy.interpolate import lagrange

### Interpolante de Lagrange
poly = lagrange (x_i, y_i)
print(poly)

    2
-2 x + 10.33 x - 6.333

Para evaluar dicho polinomio en el conjunto de puntos en que hemos dividido el intervalo \([0,5]\) usamos la clase polynomial de numpy. La función Polynomial recibe los coeficientes del polinomio en orden creciente y devuelve para cada valor de \(x\) su imagen.

from numpy.polynomial.polynomial import Polynomial

### Representación gráfica
ax = plt.scatter(x_i,y_i, color="red")
plt.plot(x,Polynomial(poly.coef[::-1])(x), color="blue")
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title('Interpolante polinómico de Lagrange', fontsize=16)

Text(0.5, 1.0, 'Interpolante polinómico de Lagrange')
../../_images/4add5448b89ada259bb597aaaa799697f38dc36f0349f4a7d7a963f378e40e92.png