4. Derivación Numérica.

Partiremos del polinomio interpolador de Lagrange en \(N+1\) puntos de interpolación equiespaciados \(\{x_i\} \text{ con } i= 0,...,N \) y de los valores de la función a aproximar en dichos puntos \(\{f(x_i)\} \text{ con } i= 0,...,N \). Vimos que dados \(N+1\) puntos \(\{(x_0,f(x_0)), (x_1,f(x_1)), ..., (x_N, f(x_N))\}\) podemos construir una aproximación polinómica a la funciín \(f(x)\) utilizando los polinomios de Lagrange:

(4.1)\[\begin{equation} f(x) \approx I_{N} (x) = b_{0} \ \ell_{0} (x) \ + \ b_{1} \ \ell_{1} (x) \ + \ \cdots \ + \ b_{N} \ \ell_{N} (x) = \ \sum_{j = 0}^{N} \ b_j \ell_{j} (x) \end{equation}\]

La forma \(I_{N} (x)\) se conoce como interpolante de Lagrange, los polinomios \(\ell_{j} (x)\) son los polinomios de Lagrange que tienen la expresión siguiente:

(4.2)\[\begin{equation} \displaystyle \ell_{j} (x) \ = \ \displaystyle \overset{N}{\underset{\begin{subarray}{l} i = 0 \\ i \neq j \end{subarray} }{\prod}} \ \frac{(x - x_i)}{(x_j - x_i)} . \end{equation}\]

y los coeficientes \(b_j\) verifican:

\[ b_j \ = \ f (x_j) , \]

con lo que, el polinomio interpolante, resulta ser:

(4.3)\[\begin{equation} \displaystyle I_{N} (x) \ = \ \sum_{j = 0}^{N} \ f (x_j) \ \ \displaystyle \overset{N}{\underset{\begin{subarray}{l} i = 0 \\ i \neq j \end{subarray} }{\prod}} \ \frac{(x - x_i)}{(x_j - x_i)} . \end{equation}\]

Si queremos utilizar el polinomio interpolante para aproximar la derivada basta derivar a ambos lados de la igualdad:

(4.4)\[\begin{equation} f'(x) \approx I'_{N} (x) =\ \sum_{j = 0}^{N} \ f (x_j) \ell'_{j} (x) \end{equation}\]

y lo mismo para aproximar la derivada segunda:

(4.5)\[\begin{equation} f''(x) \approx I''_{N} (x) =\ \sum_{j = 0}^{N} \ f (x_j) \ell''_{j} (x) \end{equation}\]

Estas derivadas se pueden evaluar para cualquier valor de \(x\) del dominio de definición de \(f\) aunque, en la práctica, se presentan evaluadas en los puntos de interpolación. Si \(x_k\) es un punto de interpolación, las expresiones anteriores para las derivadas primera y segunda resultan como:

(4.6)\[\begin{equation} \displaystyle f'(x_k) \ \approx \ I_N' (x_k) \ = \ \sum_{j = 0}^N \ f (x_j) \ \ell_j' (x_k) , \label{aproximacion_derivada_primera_x_k} \end{equation}\]

y

(4.7)\[\begin{equation} \displaystyle f''(x_k) \ \approx \ I_N'' (x_k) \ = \ \sum_{j = 0}^N \ f (x_j) \ \ell_j'' (x_k) . \label{aproximacion_derivada_segunda_x_k} \end{equation}\]

En las expresiones anteriores se observa para obtener las fórmulas de derivación propuestas, es necesario derivar los polinomios de Lagrange y evaluarlos en los puntos de interpolación. Otro aspecto a tener en cuenta en la obtención de estas fórmulas es que se suelen elegir números pequeños de puntos de interpolación alrededor de los puntos \(x_k\).

Vamos a empezar con las fórmulas de derivada primera numérica a partir del polinomio interpolador a través de dos puntos.

4.1. Fórmulas de derivación con 2 puntos.

Dados dos puntos \(\{(x_0,f(x_0)), (x_1,f(x_1))\}\) el polinomio interpolador va a ser, desde un punto de vista geométrico, la recta que pasa por ambos.

(4.8)\[\begin{equation} I_{1} (x) = f(x_0) \dfrac{(x-x_1)}{(x_0-x_1)} + \ f(x_1) \dfrac{(x-x_0)}{(x_1-x_0)} \end{equation}\]

Definimos \( x_1 - x_0 = \Delta x\), así, la fórmula se puede reescribir como:

(4.9)\[\begin{equation} I_{1} (x) = f(x_0) \dfrac{(x-x_1)}{(-\Delta x)} + \ f(x_1) \dfrac{(x-x_0)}{(\Delta x)} \end{equation}\]

4.1.1. Derivada primera.

Derivamos la expresión:

(4.10)\[\begin{equation} I'_{1} (x) = -\dfrac{f(x_0)}{\Delta x} + \ \dfrac{f(x_1)}{\Delta x} \end{equation}\]

Al ser un polinomio de grado 1, una recta, la derivada toma un valor constante, de modo que podemos escribir:

\[\begin{align*} f'(x_0) = f'(x_1) \approx & \dfrac{f(x_1)}{\Delta x} - \ \dfrac{f(x_0)}{\Delta x} \end{align*}\]

Esta expresión debe resultarnos familiar, si escribimos \(h = \Delta x\) y por tanto \(x_1 = x_0 + h\), resulta:

\[\begin{align*} f'(x_0) \approx & \dfrac{f(x_0 + h)- f(x_0)}{h} \end{align*}\]

En este caso no podemos seguir derivando porque al haber aproximado con una recta, la derivada primera es una constante y la segunda se anula.

4.2. Fórmulas de derivación con 3 puntos.

Partimos del polinomio interpolador con tres puntos \(\{(x_0,f(x_0)), (x_1,f(x_1)), (x_2,f(x_2))\}\):

(4.11)\[\begin{equation} I_{2} (x) = f(x_0) l_0(x) + \ f(x_1) l_1(x) + f(x_2) l_2(x) \end{equation}\]

desarrollando los polinomios de Lagrange:

(4.12)\[\begin{equation} I_{2} (x) = f(x_0) \dfrac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} + \ f(x_1) \dfrac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} + f(x_2) \dfrac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} \end{equation}\]

Como hemos escogido puntos equiespaciados: \( \{x_0, x_1, x_2 \}\) con \( x_1 - x_0 = x_2 - x_1 = \Delta x\), la fórmula se puede reescribir como:

(4.13)\[\begin{equation} I_{2} (x) = f(x_0) \dfrac{(x-x_1)(x-x_2)}{(-\Delta x)(-2\Delta x)} + \ f(x_1) \dfrac{(x-x_0)(x-x_2)}{(\Delta x)(-\Delta x)} + f(x_2) \dfrac{(x-x_0)(x-x_1)}{(2\Delta x)(\Delta x)} \end{equation}\]

4.2.1. Derivada primera.

Derivamos la expresión:

(4.14)\[\begin{equation} I'_{2} (x) = \dfrac{f(x_0)}{2(\Delta x)^2} [(x-x_1)+(x-x_2)] - \ \dfrac{f(x_1)}{(\Delta x)^2} [(x-x_0)+(x-x_2)]+ \dfrac{f(x_2)}{2(\Delta x)^2} [(x-x_0)+(x-x_1)] \end{equation}\]

Evaluamos en los puntos:

• Cuando la derivada se particulariza en en el punto de interpolación \(x_k = x_0\) se obtiene la fórmula de derivada primera descentrada adelantada:

\[\begin{align*} f'(x_0) \approx I'_{2} (x_0) & = \dfrac{f(x_0)}{2(\Delta x)^2} [(x_0-x_1)+(x_0-x_2)] - \ \dfrac{f(x_1)}{(\Delta x)^2} (x_0-x_2)+ \dfrac{f(x_2)}{2(\Delta x)^2} (x_0-x_1) = \\ &= \dfrac{f(x_0)}{2(\Delta x)^2} [(-\Delta x)+(-2\Delta x)] - \ \dfrac{f(x_1)}{(\Delta x)^2} (-2\Delta x)+ \dfrac{f(x_2)}{2(\Delta x)^2} (-\Delta x) = \\ &= -\dfrac{3f(x_0)}{2\Delta x} + \ \dfrac{2f(x_1)}{\Delta x} - \dfrac{f(x_2)}{2\Delta x} \end{align*}\]

• Cuando la derivada se particulariza en en el punto de interpolación \(x_k = x_1\) se obtiene la fórmula de derivada primera centrada:

\[\begin{align*} f'(x_1) \approx I'_{2} (x_1) & = \dfrac{f(x_0)}{2(\Delta x)^2} (x_1-x_2) - \ \dfrac{f(x_1)}{(\Delta x)^2} [(x_1-x_0)+(x_1-x_2)]+ \dfrac{f(x_2)}{2(\Delta x)^2} (x_1-x_0) = \\ &= \dfrac{f(x_0)}{2(\Delta x)^2} (-\Delta x) - \ \dfrac{f(x_1)}{(\Delta x)^2} (\Delta x-\Delta x)+ \dfrac{f(x_2)}{2(\Delta x)^2} (\Delta x) = \\ &= -\dfrac{f(x_0)}{2\Delta x} + \ \dfrac{f(x_2)}{2\Delta x} \end{align*}\]

• Por último cuando la derivada se particulariza en en el punto de interpolación \(x_k = x_2\) se obtiene la fórmula de derivada primera descentrada atrasada:

\[\begin{align*} f'(x_2) \approx I'_{2} (x_2) & = \dfrac{f(x_0)}{2(\Delta x)^2} (x_2-x_1) - \ \dfrac{f(x_1)}{(\Delta x)^2} (x_2-x_0)+ \dfrac{f(x_2)}{2(\Delta x)^2} [(x_2-x_0)+(x_2-x_1)] = \\ &= \dfrac{f(x_0)}{2(\Delta x)^2} (\Delta x) - \ \dfrac{f(x_1)}{(\Delta x)^2} (2\Delta x)+ \dfrac{f(x_2)}{2(\Delta x)^2} (2\Delta x + \Delta x) = \\ &= \dfrac{f(x_0)}{2\Delta x} - \ \dfrac{2f(x_1)}{\Delta x} + \dfrac{3f(x_2)}{2\Delta x} \end{align*}\]

4.2.2. Derivada segunda.

En esta ocasión si podemos calcular una aproximación de la derivada segunda a partir del polinomio interpolador de Lagrange de segundo orden.

Si volvemos a derivar \(I'_{2} (x)\) con respecto a x obtenemos:

(4.15)\[\begin{equation} I''_{2} (x) = \dfrac{f(x_0)}{(\Delta x)^2} - \ \dfrac{2 f(x_1)}{(\Delta x)^2} + \dfrac{f(x_2)}{(\Delta x)^2} \end{equation}\]

El valor aproxiomado es constante e independiente del punto en qué se aplique.

(4.16)\[\begin{equation} f''(x_0) = f''(x_1) = f''(x_2) \approx \dfrac{1}{(\Delta x)^2} \left(f(x_0) -2 f(x_1) + f(x_2)\right) \end{equation}\]

4.3. Implementación en Python.

Vamos a empezar con un primer ejemplo en una función sencilla:

\[ f_1 (x) \ = sin(x), \]

supongamos que tenemos 9 puntos de interpolación equiespaciados en el intervalo \([-\pi, \pi]\) y a través de ellos vamos a aproximar el valor de la derivada en dichos puntos.

# Importamos los módulos necesarios
import numpy as np 
import scipy as sp
from matplotlib import pyplot as plt 
n = 9
m = 100
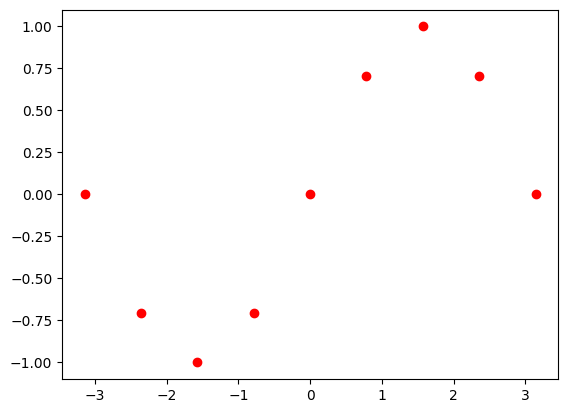
x_i = np.linspace(-np.pi, np.pi, n)
y_i = np.sin(x_i)
z_i = np.cos(x_i)

x = np.linspace(min(x_i)-0.02, max(x_i)+0.02, m)

### Representación gráfica
ax = plt.scatter(x_i,y_i, color="red")

Lo primero que vamos a probar va a ser la aproximación de la derivada usando el conjunto de puntos de interpolación a través de la fórmula:

(4.17)\[\begin{equation} f'(x) \approx I'_{N} (x) =\ \sum_{j = 0}^{N} \ f (x_j) \ell'_{j} (x) \end{equation}\]

Necesitamos calcular \(\ell'_{j} (x)\). Teniendo en cuenta que:

(4.18)\[\begin{equation} \displaystyle \ell_{j} (x) \ = \ \displaystyle \overset{N}{\underset{\begin{subarray}{l} i = 0 \\ i \neq j \end{subarray} }{\prod}} \ \frac{(x - x_i)}{(x_j - x_i)} . \end{equation}\]

podemos derivar para obtener:

(4.19)\[\begin{equation} \displaystyle \ell'_{j} (x) \ = \ \displaystyle \overset{N}{\underset{\begin{subarray}{l} i = 0 \\ i \neq j \end{subarray} }{\sum}} \frac{1}{(x_j - x_i)} \overset{N}{\underset{\begin{subarray}{l} k = 0 \\ k \neq j \\ k \neq i \end{subarray} }{\prod}} \ \frac{(x - x_k)}{(x_j - x_k)} . \end{equation}\]

que podemos implementar en Python prestando atención a los índices del productorio anidado al sumatorio

"""
# Polinomio de Lagrange L_j(x)
def L_j(j, x_i, x):
    n = np.size(x_i)
    Lj = 1.
    for i in range(n):
        if i!=j: Lj *= (x-x_i[i])/(x_i[j]-x_i[i]) 
    return Lj

def I_N(x, x_i, y_i):
    n = np.size(x_i)
    S = 0.
    for i in range(n):
        S += y_i[i]*L_j(i, x_i, x)
    return S
"""

# Derivada primera del polinomio de Lagrange L'_j(x)
def L_der_j(j, x_i, x):
    n = np.size(x_i)
    Lj = 0.
    for i in range(n):
        prod = 1.
        for k in range(n):
            if (k!=j) & (k!=i):
                prod *= (x-x_i[k])/(x_i[j]-x_i[k]) 
        if i!=j: Lj += prod/(x_i[j]-x_i[i]) 
    return Lj

def I_der_N(x, x_i, y_i):
    n = np.size(x_i)
    S = 0.
    for i in range(n):
        S += y_i[i]*L_der_j(i, x_i, x)
    return S

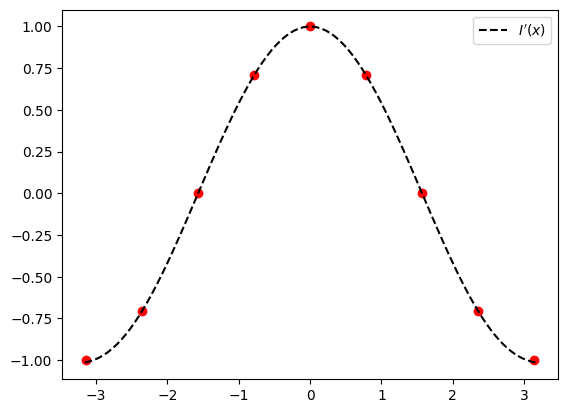
Para ver si la implementación es correcta comparamos la aproximación de la derivada a partir de los puntos de la función \(f(x) = sin(x)\) con el valor del \(cos(x)\)

### Representación gráfica
fig = plt.figure()
fig, ax = plt.subplots()
ax.scatter(x_i,z_i, color="red")
ax.plot(x,I_der_N(x, x_i, y_i), color="black",linestyle='--',label="$I'(x)$")
ax.legend()
plt.show()

<Figure size 640x480 with 0 Axes>

Esta forma de derivar no deja de ser un ejercicio interesante. Normalmente el problema numérico que vamos a resolver es el cáculo de la derivada de una función en un punto a partir del valor de la función en puntos próximos. Es decir la implementación de estas aproximaciones en funciones de Python cuando los argumentos son la función \(f(x)\) y un punto de evaluación \(x_j\).

Vamos a resumir las fórmulas de las derivadas numéricas para una función \(f:\mathbb{R} \rightarrow \mathbb{R}\) en un punto \(x_j\), obtenidas a partir de tres puntos de interpolación de una partición equiespaciada.

• Derivada primera centrada:

\begin{equation} f' (x_j) \approx \frac{1}{2 \Delta x} \left( f (x_j + \Delta x) - f (x_j - \Delta x) \right) . \end{equation}

• Derivada primera descentrada adelantada:

\begin{equation} f' (x_j) \approx \frac{1}{2 \Delta x} \left( - 3 f (x_j) + 4 f (x_j + \Delta x) - f (x_j + 2 \Delta x) \right) . \end{equation}

• Derivada primera descentrada atrasada:

\begin{equation} f' (x_j) \approx \frac{1}{2 \Delta x} \left( 3 f (x_j) - 4 f (x_j - \Delta x) + f (x_j - 2 \Delta x) \right) . \end{equation}

• Derivada segunda centrada:

\begin{equation} f'' (x_j) \approx \frac{1}{(\Delta x)^2} \left( f (x_j + \Delta x) - 2f (x_j) + f (x_j - \Delta x) \right) . \end{equation}

Podemos implementar cada una de ellas en una función diferente:

def f_prima_centrada_3_puntos(x, dx, f):
    derivada = (f(x+dx)-f(x-dx))/(2*dx)
    return derivada

def f_prima_adelantada_3_puntos(x, dx, f):
    derivada = (-3.*f(x)+4.*f(x+dx)-f(x+2*dx))/(2*dx)
    return derivada

def f_prima_atrasada_3_puntos(x, dx, f):
    derivada = (3.*f(x)-4.*f(x-dx)+f(x-2*dx))/(2*dx)
    return derivada

def f_prima_segunda_3_puntos(x, dx, f):
    derivada = (f(x+dx)-2.*f(x)+f(x-dx))/(dx**2)
    return derivada

def f_seno(x):
    return np.sin(x)

### Representación gráfica
fig = plt.figure()
fig, ax = plt.subplots()

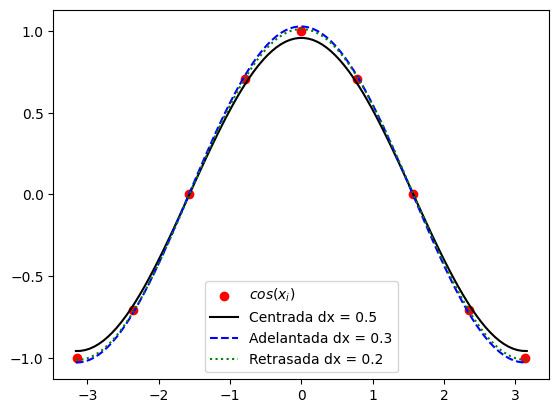
ax.scatter(x_i,z_i, color="red",label='$cos(x_i)$')
ax.plot(x,f_prima_centrada_3_puntos(x, 0.5, f_seno), color="black",label='Centrada dx = 0.5')
ax.plot(x,f_prima_adelantada_3_puntos(x, 0.3, f_seno), color="blue",linestyle='dashed',label='Adelantada dx = 0.3')
ax.plot(x,f_prima_atrasada_3_puntos(x, 0.2, f_seno), color="green",linestyle='dotted',label='Retrasada dx = 0.2')
ax.legend()

plt.show()

<Figure size 640x480 with 0 Axes>

4.4. Matrices de derivación.

Vamos a suponer ahora que queremos calcular la derivada numerica de una función \(f(x)\) en un intervalo \(\left[ a, b \right]\). El proceso que seguiremos será discretizar el intervalo en un conjunto de puntos equiespaciados \(\left[ a=x_0, x_1, x_2,...,x_N = b \right]\) con \(\Delta x = x_{j+1}-x_j \) y en cada uno de los puntos calcularemos su derivada numérica con las fórmulas ya vistas.

Si pensamos en forma vectorial-matricial tenemos por una parte el vector de puntos equiespaciados en que hemos discretizado \(\left[ a, b \right]\):

(4.20)\[\begin{equation} X = \begin{pmatrix} x_0\\ x_1\\ x_2\\ \vdots \\ x_N \end{pmatrix} \end{equation}\]

el vector \(F\) donde guardamos el valor de la funcion \(f(x)\) en los puntos de \(X\):

(4.21)\[\begin{equation} F = \begin{pmatrix} f(x_0)\\ f(x_1)\\ f(x_2)\\ \vdots \\ f(x_N) \end{pmatrix} \end{equation}\]

y queremos construir el vector \(dF\) con las aproximaciones de la derivada \(f'(x)\) en los puntos de \(X\) a partir de las fórmulas ya vistas. Supongamos, por ejemplo, que voy a emplear la fórmula de derivada centrada con tres puntos para aproximar la derivada en cada punto. Es decir que:

(4.22)\[\begin{equation} dF(i) = f'(x_i) \approx \frac{1}{2 \Delta x} \left( f (x_{i+1}) - f (x_{i-1}) \right) \end{equation}\]

Esta fórmula será válida para todos los puntos ‘interiores’ del vector \(i = 1,...,N-1\) ya que para \(x_0\) no existe \(x_{i-1}\) y para \(x_N\) no existe \(x_{i+1}\). En los extremos tendremos que ‘descentrar el esquema’ y utilizar derivada adelantada en \(x_0\) y derivada atrasada en \(x_N\):

(4.23)\[\begin{align} dF(0) = f'(x_0) & \approx \frac{1}{2 \Delta x} \left( - 3 f (x_0) + 4 f (x_1) - f (x_2) \right) \\ dF(N) = f'(x_N) & \approx \frac{1}{2 \Delta x} \left( 3 f (x_N) - 4 f (x_{N-1}) + f (x_{N-2}) \right) \end{align}\]

Si escribimos en forma matricial las ecuaciones anteriores tendremos:

(4.24)\[\begin{align} \frac{1}{2 \Delta x} \begin{pmatrix} -3 & 4 & -1 & 0 & \dots & 0\\ -1 & 0 & 1 & 0 & \dots & 0\\ 0 & -1 & 0 & 1 & \dots & 0\\ \vdots & & \ddots &\ddots & & \vdots \\ 0 &\dots & -1 & 0 & 1 & 0\\ 0 &\dots & 0 & -1 & 0 & 1\\ 0 &\dots & 0 & 1 & -4 & 3 \end{pmatrix} \begin{pmatrix} f(x_0)\\ f(x_1)\\ f(x_2)\\ \vdots \\ f(x_{N-2})\\ f(x_{N-1})\\ f(x_N) \end{pmatrix} = \begin{pmatrix} dF(0)\\ dF(1)\\ dF(2)\\ \vdots \\ dF(N-2)\\ dF(N-1)\\ dF(N) \end{pmatrix} \end{align}\]

Vamos a probar su funcionamiento derivando la función:

\[ f_1 (x) \ = cos(x), \]

en el intervalo \([0, \pi]\) utilizando 21 puntos para discretizar dicho intervalo.

n = 11
x_i = np.linspace(0, np.pi, n)
dx = np.pi/(n-1)
# Defino la matriz de derivación D
D = np.zeros((n,n), dtype = float)
D[0,0:3] = np.array([-3.,4.,-1.])
for i in range(1,n-1):
    D[i,i-1] = -1.
    D[i,i+1] = 1.
D[n-1,n-3:n] = np.array([1.,-4.,3.])    
D /= (2*dx)

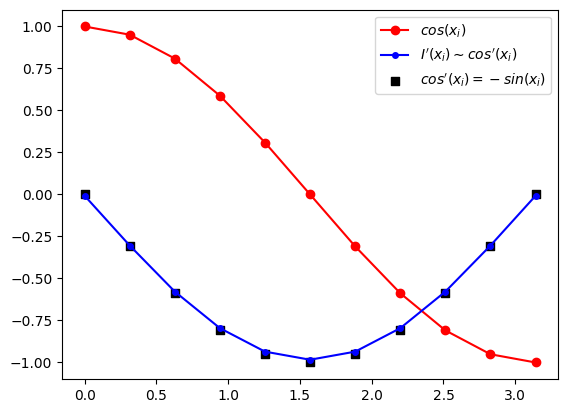
f_i = np.cos(x_i)
dF_i = np.matmul(D,f_i)

### Representación gráfica
fig = plt.figure()
fig, ax = plt.subplots()

ax.plot(x_i,f_i, color="red",marker='o',label='$cos(x_i)$')
ax.plot(x_i,dF_i, color="blue",marker='o',markersize=4, label="$I'(x_i) \sim cos'(x_i)$")
ax.scatter(x_i,-np.sin(x_i), color="black",marker='s',s=40,label="$cos'(x_i)=-sin(x_i)$")
ax.legend()

plt.show()

<Figure size 640x480 with 0 Axes>